发布时间:2024-07-19
近日,59599aa美高梅、上海自主智能无人系统科学中心严钢教授团队在复杂系统隐含随机动力学的可解释推理方面取得新进展,研究成果以“Learning interpretable dynamics of stochastic complex systems from experimental data”为题发表于《自然·通讯》(Nature Communications)。
实际复杂系统不仅表现出高动态和非线性,而且具有内稟随机性,其动力学行为适宜用随机微分方程(SDE)进行定量描述。然而,很多实际复杂系统的内在动力学机制尚不清楚,因此需要从观测数据中逆向推断隐含的SDE。这是一个具有挑战性的反问题。近年来,数据驱动的动力系统方程推理得到了快速发展,已成为科学智能(AI for Science)的一个重要方向,但仍存在诸多不足。例如,很多方法仅关注单体动力学或确定性的动力学,较少考虑系统的随机性,且主要在模拟的标准数据集上进行方法性能比较,鲜少应用于实际复杂系统的实验数据。
为此,严钢教授团队将前期提出的方法框架进行了拓展,新得到的朗之万图网络(Langevin Graph Network, LaGNA)能够对具有随机性的复杂网络系统动力学进行可解释推理。该LaGNA方法通过构建信息传递的图结构,在图的各节点和连边上嵌入神经网络模块,分别捕捉系统的自身演化、耦合效应和随机波动,实现对随机系统行为的预测,最后通过稀疏辨识技术打开各神经网络模块的黑盒子,推断出随机微分方程组的简洁数学表达式(图1)。通过与已有的5种方法进行比较,LaGNA在随机动力学推理方面展现出显著优势。
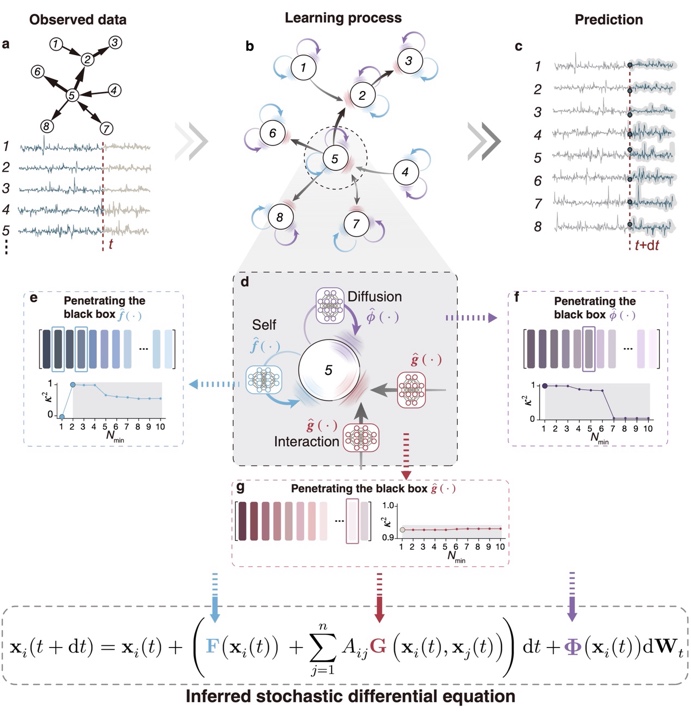
图1:LaGNA推理框架示意图。(a)输入观测数据;(b, d)构建信息传递的图结构,并在各节点和连边上分别嵌入的神经网络模块;(c)通过训练使该架构具有对随机系统演化的预测能力;(e-g)最后利用稀疏辨识技术打开各神经网络模块的黑盒子,得到隐含的随机微分方程组,实现可解释推理。
该研究将提出的LaGNA方法用于两个实际复杂系统的推理:自然界的鸟类集群行为与大脑中的tau蛋白病理扩散过程(图2)。基于实验观测数据,LaGNA成功推理出鸟群协同飞行的随机动力学机制,得到的方程在形式上与经典的二阶Vicsek模型相类似,表明Vicsek模型不仅仅是一个简化理论模型而是能够刻画真实集群行为。基于tau蛋白病理在小鼠大脑中传播的实验数据,LaGNA推理出tau蛋白随机扩散方程,该方程的每一项均有对应的生物学解释,并发现了基因突变小鼠的不同病理动态特征。两个实例展现了方法的适用性,推理结果的可解释性有助于揭示实际复杂系统的内在机理,为复杂系统控制等后续任务提供了模型基础。
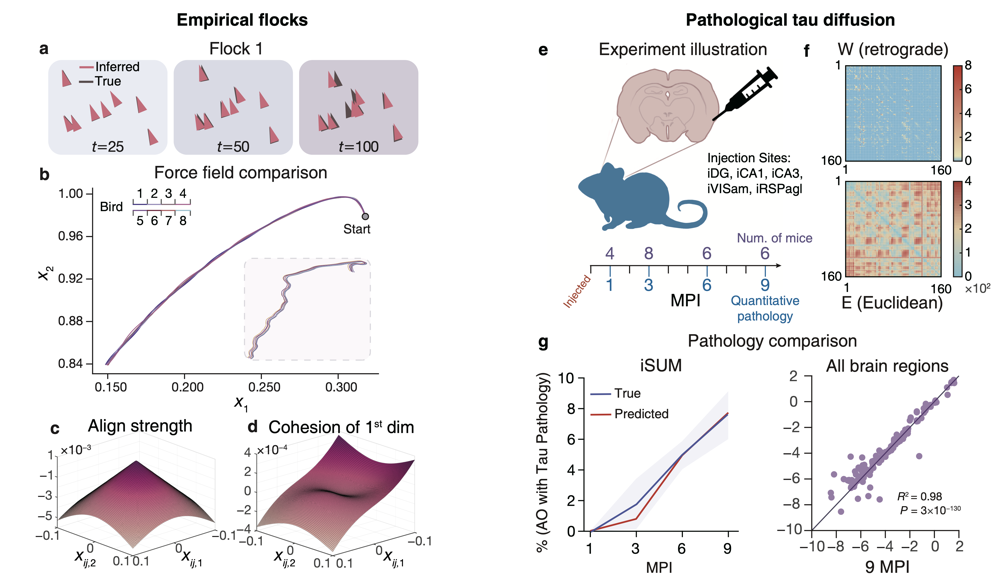
图2:LaGNA方法应用于两个实际复杂系统的可解释推理。(a-d)基于实验观测数据推断鸟群协同飞行的隐含随机动力学方程;(e-g)基于阿尔兹海默症病理tau蛋白在小鼠大脑中传播的实验数据,推理得到tau蛋白随机扩散方程,具有预测能力和可解释性。
59599aa美高梅高婷婷博士是该论文第一作者,严钢教授是通讯作者,合作者还包括以色列巴伊兰大学的Barzel教授。该研究得到了国家基金委和上海市的项目资助。